"The magic of compounding returns is the biggest mathematical discovery of all time." – Benjamin Graham

Visualize compounding as a little snowball that rolls down a very long hill and in the process it continues to collect snows to become a huge snowball.

Nature of compounding can be condensed to three characteristics:

• It's exponential

• It has a function of time and rate of return

• It exhibits positive asymmetry

Exponential

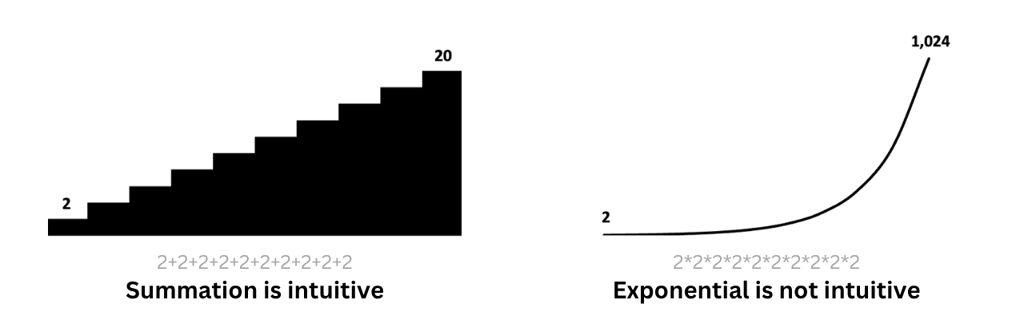
When you add two with two, you know the result intuitively that it's four. Now you continue to add more twos and it's not hard to figure out. Do the same thing for multiplication. Multiply two with two, and you know it's four. Now multiply two with four, you know it's eight. Continue to do the process and you will soon reach a number big enough that you will have to take a pause before figuring out the result. Summation is intuitive but the function of exponential is not intuitive. We often can't comprehend how big the numbers can turn out after enough compounding.

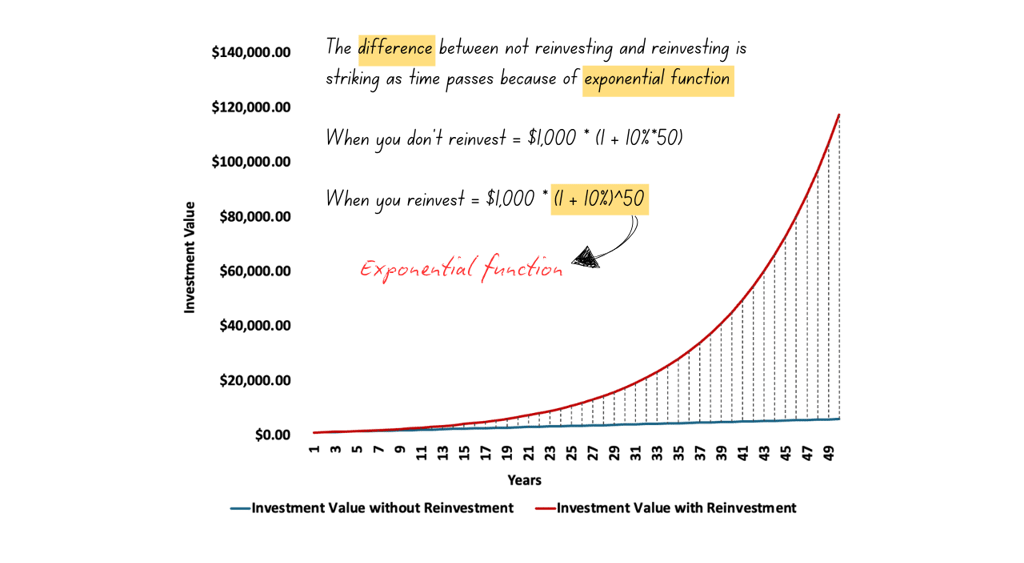
Let's say, you make two investments in same securities starting with $1,000 each for 50 years.

• In one investment, you don’t reinvest the annual income (you get 10.0% on your initial investment every year end).

• In another investment, you reinvest the annual income with same rate of return.

The difference between not reinvesting and reinvesting is striking as time passes because of exponential function. When you don’t reinvest, your $1,000 grows to $6,000 after 50 years ($1,000 *(1 + 10%*50)). When you reinvest, the value grows to $117,391 ($1,000 * (1 + 10%)^50).

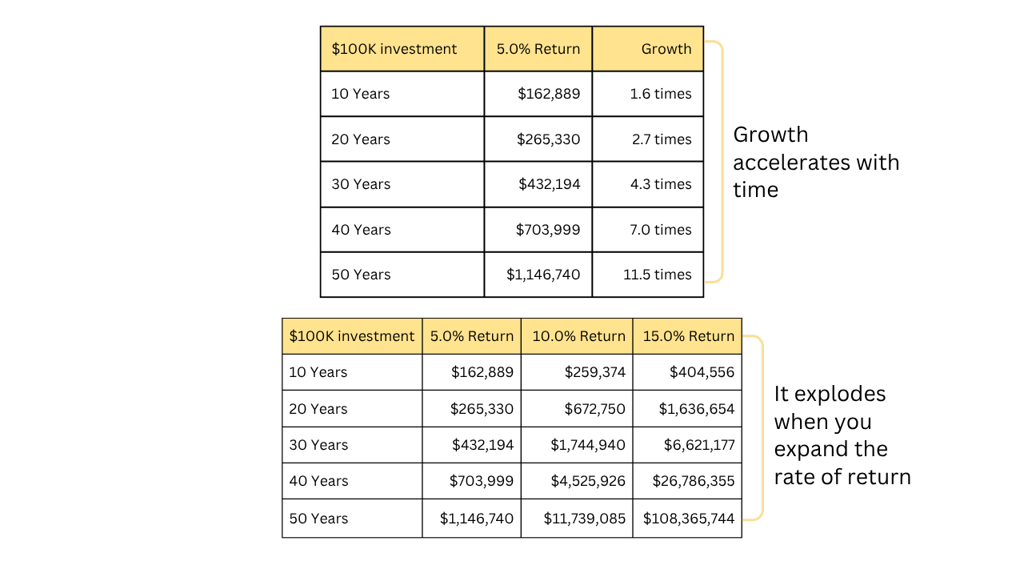
Function of Time and Rate of Return

When you let something compound for enough time, it is equivalent to magic. Compounding is a function of time and rate of return. The more time and rate of return expands, the more steepening the growth becomes.

Positive Asymmetry

Let’s say, you buy Stock A at $100 and it compounds 10.0% every year for next 10 years. What happens? The price of the stock increases at a increasing rate.

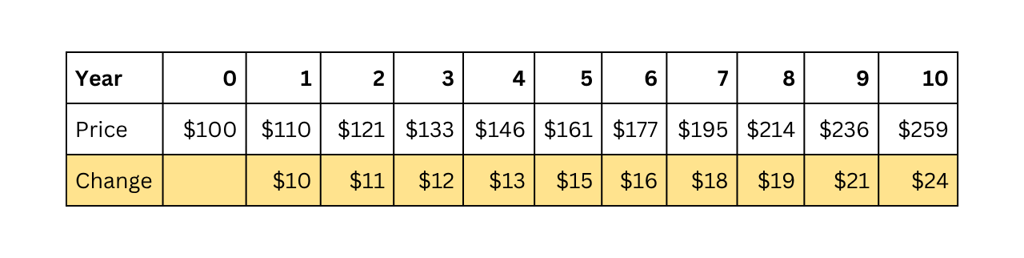
Assume, you buy Stock B at $100 and it declines 10.0% every year for next 10 years. The price of the stock decreases at a decreasing rate.

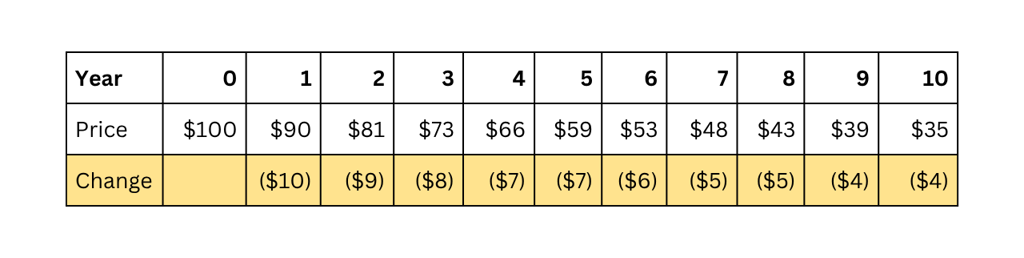
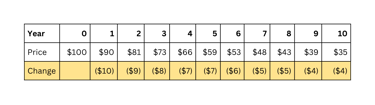
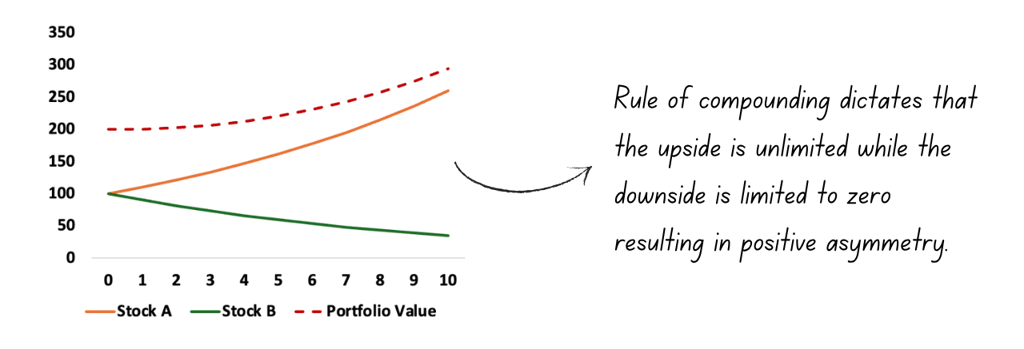
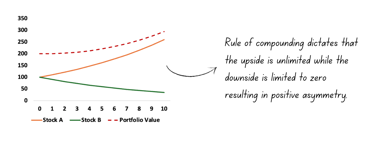
If you build your portfolio with these two stocks:

Now, consider a market with five stocks, each starting with $100 in value. Stock A starts with $100 in value and rest of the market starts with $400 in value.We assume stock A is a great business that compounds shareholder wealth at an annual 10.0% rate for next 20 years while rest of the market declines 10.0% each year in the same timeline.

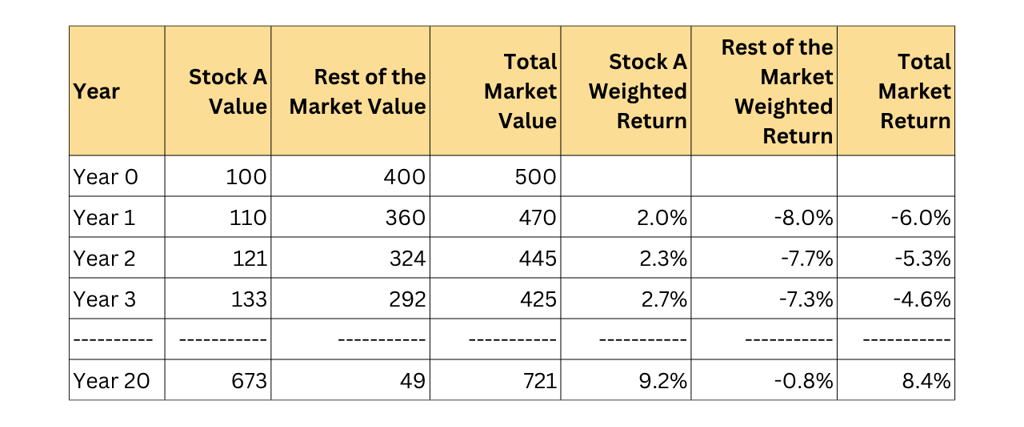
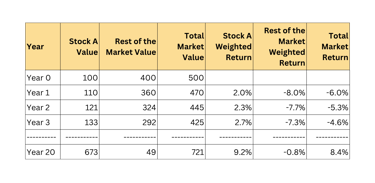
At the end of first year, total market value falls to $470 with a total net return of negative 6.0%.

After 20 years of compounding, stock A reaches a value of $673, while total market value reaches $721. In later years, the winning stock dominates the market return.

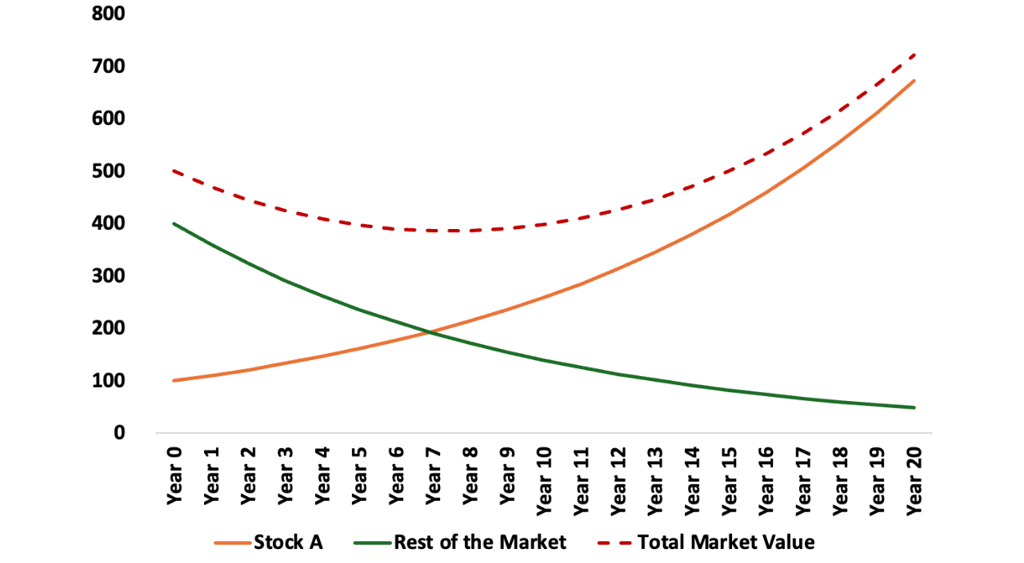
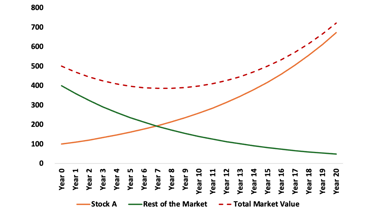
• Rule of compounding dictates that the upside is unlimited while the downside is limited to zero.

• When something grows at a certain rate for a long time, it grows at an increasing rate and when something continues to decline at a certain rate, it declines at a decreasing rate resulting in positive asymmetry.

• Over the years, the winning stocks dominate the market return and the losing ones fade into insignificance.

• Any incremental change in the winning stock, after enough compounding, has outsized impact in the overall return of the market.